Probabilidade é o cálculo das chances de algo acontecer.
Por exemplo, se jogar uma moeda para cima, quais as chances de cair o número 6?
Se você respondeu “nenhuma”, então você já provou que sabe alguma coisa do assunto. Muito bem.
Só que os problemas vão ficando cada vez mais complexos e você já deve ter percebido que não existe uma fórmula para responder os exercícios. Você precisa interpretar e usar a sua caixola para resolver.
Isso traz um grande desafio para a maioria dos alunos.
Se você já vai mal em matemática, não ter uma fórmula torna as coisas ainda mais difíceis.
E sabendo disso, trago aqui uma solução.
Vou demonstrar um PASSO A PASSO de como resolver QUALQUER exercício de probabilidade. Se você entender bem tudo isso, vai conseguir virar o mais novo crânio da sua turma.
Índice de Conteúdos
- Pré-Requisitos
- Os 5 Passos Mágicos
- Exemplo 1 – Entendendo os passos básicos
- Exemplo 2 – Universos e Permutações
- Exemplo 3 – Chances de passar no Vestibular
- Exemplo 4 – Probabilidade sem suor
- Exemplo 5 – Esse parece diferente
- Conclusão
Pré-Requisitos

Infelizmente nem tudo são flores. Em matemática é assim mesmo: todo conhecimento depende de outros conhecimentos. Felizmente eu também vou deixar os links ensinando cada um destes pontos.
Aqui você vai precisar saber:
- Multiplicação e Soma de Frações
- Permutação com Repetição
- Princípios básicos de Contagem
- Princípio básico da Probabilidade
Já sabe dessas coisas? Então pule para os 6 Passos.
Princípio Básico da Contagem (E/OU)
Imagine que você tenha 3 camisetas E 2 calças. Quantas possibilidades são possíveis?
No caso, como temos que formar um par, utilizamos a multiplicação. E = multiplicação.
Logo, 3 * 2 = 6 possibilidades.
Se tivermos 3 calças OU 2 bermudas, fazemos uma soma. 3+2 = 5. OU = soma.
A mesma coisa acontece nas probabilidades. Se você participa de um sorteio em uma roleta e tem 10% de chances de ganhar uma caneta OU 20% de ganhar um jogo, você tem 30% de ganhar algo.
Já se jogar duas roletas separadas, você tem 10% de ganhar uma caneta E 20% de ganhar um jogo. Ou seja, a chance de ganhar ambos é de 1/10 * 2/10 = 2/100 apenas, ou 2%.
Princípio básico da Probabilidade (N/T)
Toda probabilidade segue esse formato:
- Em cima colocamos as N possibilidades do que queremos
- Embaixo colocamos as T possibilidades totais.
Logo: N / T é o formato da probabilidade.
No caso, da jogada de uma moeda, embaixo são 2 possibilidades totais: cara ou coroa.
Em cima, se quero tirar cara, tenho 1 possibilidade. Ou seja: 1/2
Se fosse um dado, seria diferente. Seriam 6 possibilidades TOTAIS. Se eu quisesse tirar o número 4, seria 1/6 chances. Se eu quisesse números pares, seriam 3/6 chances.
Ok, mas não se empolgue, porque só essa fórmula não vai te ajudar em nada nos exercícios.
Probabilidade em 5 Passos

Como o prometido, vou passar rapidamente os 5 passos para você resolver QUALQUER exercício de probabilidade.
Vamos primeiros visualizar o processo e depois aprofundar, então se tiver dúvidas, apenas as anote e prossiga. Caso o artigo não resolva a sua dúvida, deixe um comentário! Não fique com vergonha.
Faça os exemplos como se fossem exercícios. Caso tenha dúvidas, veja qual foi o processo e tente entender tudo o que aconteceu.
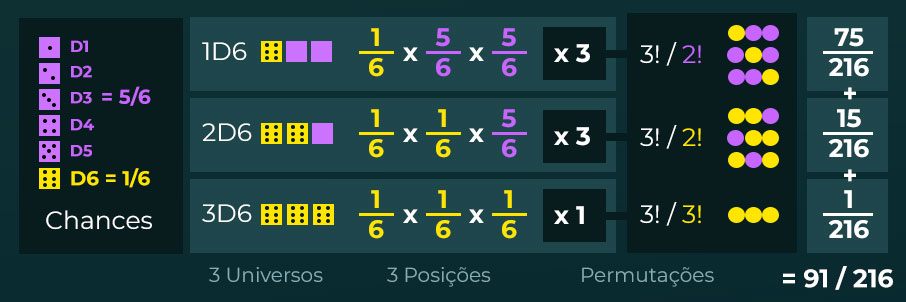
Exemplo 1 – Entendendo o Processo
“Qual a chance de tirar uma CARA em 3 moedas?”
Este exercício parece simples, então vamos lá.
Passo 1 – Quais as chances (ou probabilidades) individuais?
- Qual a chance de tirar Cara? Chance de 1/2
- Qual a chance de tirar Coroa? Chance de 1/2
Passo 2 – Quantas posições ou jogadas?
Aqui você deve saber quantas posições, jogadas ou vezes o caso acontece. No caso, são 3 jogadas de moedas.
Passo 3 – Quais os Universos Paralelos desejados e as suas chances
Quando digo Universo, quero dizer quantas realidades paralelas eu devo calcular. São situações um OU outro. Por exemplo, se o exercício pedisse PELO MENOS uma cara, teríamos 3 opções:
- 1 Cara e 2 Coroas
- OU 2 Caras e 1 Coroa
- OU 3 Caras
Mas no nosso caso, queremos apenas 1 CARA e 2 COROAS, ou seja temos só 1 Universo.
Neste Universo são 3 posições que se multiplicam, pois temos o valor da primeira moeda E o valor da segunda E o valor da terceira.
__ . __ . __
Logo, temos a chance de CARA * chance de COROA * chance de COROA.
Se substituirmos cada uma destas posições com as chances de cada opção, teremos 1/2 * 1/2 * 1/2 = 1/8 chances.
Passo 4 – Existem Permutações?
Mas e se a cara cair só na segunda ou terceira moeda? Isso significa que precisamos permutar os resultados.
Você pode ter CKK ou KCK ou KKC.
A quantidade de permutações pode ser descoberta pela fórmula de permutação com repetição. No caso: 3! / 2! = 3.
Ou seja, temos 3 * 1/8 = 3/8 chances.
Bônus – Permutações com repetições
Na verdade, quando falamos de permutações também estamos falando de “Universos Paralelos”, pois elas caem no caso do “OU”.
Só que fazemos permutações porque acontecem repetições desses “ou”. Ao invés de somar 1/8 + 1/8 + 1/8, podemos fazer 3 vezes 1/8.
Como fica difícil descobrir permutações complexas, aconselho que você aplique SEMPRE a fórmula da Permutação com Repetição:
Permutação de Posições Totais
———————————————-
Permutação das Repetições
Lembrando que permutação significa FATORIAL. Ou seja, no caso temos: 3! / 2! = 3
- Se fossem 2 caras em 10 moedas, seriam: CCKKKKKKKK, ou seja: 10! / 2! 8! = 45
Neste caso temos 10 posições totais, 2 repetições de CARA e 8 repetições de COROA.
- Se fossem dois números 6 em cinco dados, teríamos 66NNN = 5! / 2! 3! = 10
Neste caso temos 5 posições totais, 2 repetições do seis e 3 repetições de quaisquer outros números.
Passo 5 – Some as possibilidades dos Universos
No caso, só temos um Universo, então a resposta final é 3/8.
Se tivéssemos mais Universos, teríamos que somar todas as probabilidades.
Foi fácil? Agora vamos fazer outros exemplos para fixar o método.
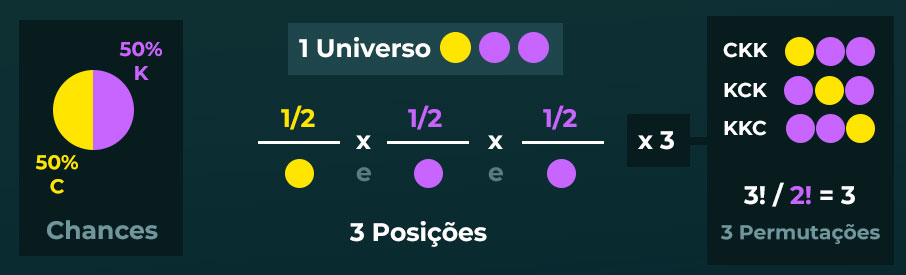
Exemplo 2 – Permutações e Universos
“Qual a chance de tirar pelo menos um SEIS em 3 jogadas de dados?”
Agora vamos complicar um pouco as coisas adicionando o conceito de permutações e Universos de possibilidades.
1- As chances são de 1/6 para o número 6, e 5/6 para o resto
2- Temos 3 posições, pois são 3 jogadas.
3- Temos 3 Universos paralelos desejados:
- 1D – Apenas um dado 6 = 1/6 * 5/6 * 5/6 = 25 / 216
- 2D – Apenas dois dados 6 = 1/6 * 1/6 * 5/6 = 5 / 216
- 3D – Três dados 6 = 1/6 * 1/6 * 1/6 = 1 / 216
4- Quais as permutações?
- 1D = 6NN = 3! / 2! = 3 Permutações * 25 / 216 = 75 / 216
- 2D = 66N = 3! / 2! = 3 Permutações * 5 /216 = 15 /216
- 3D = 666 = 3! / 3! = 1 Permutação * 1 / 216 = 1 / 216
5 – Somando tudo e finalizando, temos (75 + 15 + 1) / 216 = 91 /216 é o resultado
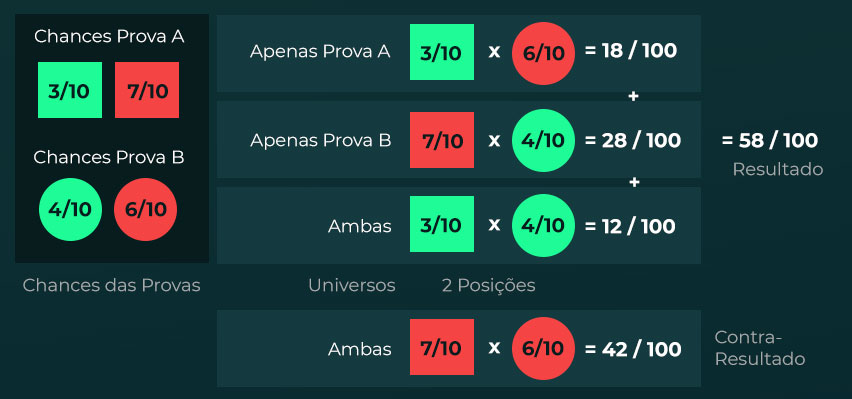
Exemplo 3 – Passar no Vestibular
“José vai prestar 2 vestibulares. No primeiro tem 30% de chances de ser aprovado e no segundo tem 40% de chances. Qual a probabilidade dele passar em pelo menos um vestibular?”
1 – Primeiro, vamos ver quais as chances de cada prova.
OBS: prefiro converter tudo para frações sempre. Lembrando que 30% = 30/100 = 3/10
- Passar em A = 3/10
- Reprovar em A = 7/10
- Passar em B = 4/10
- Reprovar em B = 6/10
2- Depois sabemos que temos 2 posições, pois são duas provas.
3- Temos 3 Universos paralelos desejados com suas possibilidades:
- Universo 1: Passar apenas em A
- Universo 2: Passar apenas em B
- Universo 3: Passar em A e B
Quais as chances em cada Universo?
- Universo 1: Passar em A * Reprovar em B = 3/10 * 6/10 = 18/100
- Universo 2: Passar em B * Reprovar em A = 4/10 * 7/10 = 28/100
- Universo 3: Passar em A * Passar em B = 3/10 * 4/10 = 12/100
4 – Não existem permutações.
5- Somando tudo:
(18 + 28 + 12) / 100 = 58 / 100 = 58% de chances
E aí, foi fácil?
Dica Bônus – Analise o Verso ou o Inverso
Algumas vezes, ao invés de calcular a chance de algo acontecer, valerá mais a pena calcular a chance de NÃO ACONTECER.
Por exemplo, aqui poderíamos ter pensado nisso: passar em pelo menos uma prova é o inverso de REPROVAR EM TODAS.
Então temos apenas um Universo para calcular: Reprovar em A * Reprovar em B
7/10 * 6/10 = 42/100
Então pegamos o inverso disso: 58/100 e temos a resposta final.
Se não entendeu, reflita um pouco e tente fazer isso no exercício
Exemplo 4 – Probabilidade sem suor
“(Enem 2017) – Uma pessoa andou por 10 semáforos. A chance de estar vermelho era de 1/3 e verde de 2/3 (ignore o sinal amarelo). Qual a chance da pessoa observar apenas um sinal verde?”
Reescrevi a questão do ENEM para deixar ela mais direta. A prova podia ser assim, não acha?
Temos 10 posições e chances de 1/3 e 2/3.
Existe apenas 1 Universo: 1 sinal verde e 9 vermelhos.
Ou seja, 2/3 * 1/3 * 1/3 * 1/3 …..
Podemos dizer que é 2/3 * (1/3)^9
(OBS: O sinal “^” significa potência. 2^3 = 2³)
Simplificando: temos a chance de 2 / (3^10)
Só que existem permutações, então temos 10 posições e 9 repetições = 10! / 9! = 10 permutações.
Resposta: 10 * 2 / (3^10)
Exemplo 5 – Esse parece diferente
“(Enem 2017) – Uma pessoa tem 50% de chances de se atrasar quando chove. Caso não chova, ela tem 25% de chances de atraso. Em um dia com 30% de chances de chuva, qual a probabilidade de uma pessoa se atrasar para o trabalho?”
Vamos lá. Este exercício requer que você tenha entendido os passos de forma não mecânica.
1- Temos várias chances:
- Chuva: 30/100
- Atraso com Chuva: 50/100
- Sem Chuva: 70/100
- Atraso sem chuva: 25/100
2- Temos 2 posições. Talvez isso não fique claro.
Existem 2 “jogadas” possíveis: chover e atrasar.
- Posição 1: Chover ou não chover
- Posição 2: Atrasar ou não atrasar
3- Temos 2 Universos Paralelos: uma realidade que chove e outra sem chuva. Quando falamos de Universos, estamos falando de um OU outro.
Eis as chances de cada Universo:
- Universo Chuva = Chove E atrasa = 30/100 * 50/100 = 15/100
- Universo Sol = Sol E Atraso = 70/100 * 25/100 = 17,5/100
4- Não existem permutações
5- Somando as probabilidades de cada Universo:
(Chove E atrasa) OU (Sol e atrasa)
(15 + 17,5) /100 = 32,5 /100 = 32,5%
Outra estratégia é desenhar (que só funciona nesses casos com “caminhos” possíveis e simples):
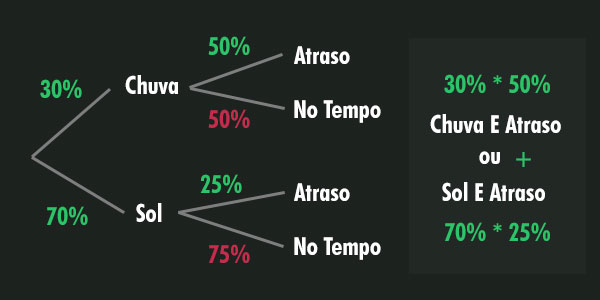
Conclusão
Se você tiver entendido bem tudo o que fizemos até agora, você não vai mais precisar seguir passo algum.
Quanto mais entender as regras, melhor vai poder quebrá-las.
Basta entender os conceitos por trás de tudo isso:
- Como calcular as chances individuais
- Multiplicar as chances individuais (E) para cada posição/jogada
- Caso existam possibilidades em paralelo (OU), some os valores
- Caso existam repetições de somas, você pode fazer uma permutação.
Eu demorei alguns dias para processar o método tradicional de probabilidades para criar este passo-a-passo, algo que consegui depois de achar um Padrão de Resolução. É uma fórmula de bolo que você cria para resolver um problema.

